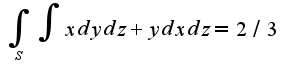Поиск
| Автор | Сообщение |
|---|---|
|
Нерадивый студент
#
17 мая 2005 |
|
|
О.А.
#
18 мая 2005 |
|
|
Stud
#
18 мая 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
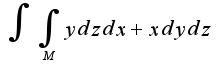 , где M - внешняя стороны пирамиды ABCD.
, где M - внешняя стороны пирамиды ABCD.
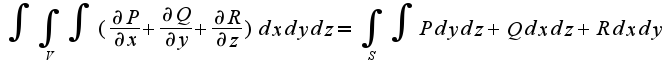 , где S-граница области V. Для данного примера
, где S-граница области V. Для данного примера 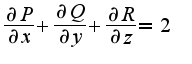 Поэтому получим, что
Поэтому получим, что 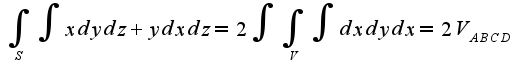 , где
, где 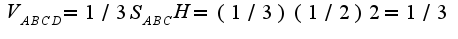 Тогда
Тогда