Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
Поиск| Автор | Сообщение |
|---|---|
|
kiss off
#
8 дек 2009 |
|
|
lenochka)
#
9 дек 2009 |
|
|
Ольга
#
14 дек 2009 |
|
|
О.А.
#
14 дек 2009 |
|
|
Танечка
#
16 дек 2009 |
|
|
О.А.
#
16 дек 2009 |
|
|
Евгений
#
16 дек 2009 |
|
|
Viktor
#
22 дек 2009 |
|
|
О.А.
#
22 дек 2009 |
|
|
Дарья
#
24 дек 2009 |
|
|
О.А.
#
24 дек 2009 |
|
|
Дарья
#
24 дек 2009 |
|
|
О.А.
#
24 дек 2009 |
|
|
Дарья
#
24 дек 2009 |
|
|
О.А.
#
24 дек 2009 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
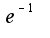
 , в данном случае на
, в данном случае на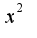 , получим
, получим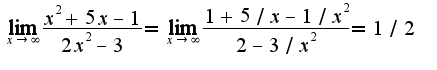 т.к.
т.к.