Поиск
| Автор | Сообщение |
|---|---|
|
Евгений
#
6 ноя 2007 |
|
|
Евгений
#
14 апр 2008 |
|
|
О.А.
#
9 апр 2007 |
|
|
Евгений
#
6 ноя 2007 |
|
|
О.А.
#
6 ноя 2007 |
|
|
Евгений
#
6 ноя 2007 |
|
|
Евгений
#
6 ноя 2007 |
|
|
Анатолий
#
6 ноя |
|
|
О.А.
#
6 ноя 2007 |
|
|
Евгений
#
6 ноя 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
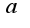 - фиксированное число)
- фиксированное число)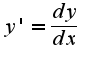 поэтому
поэтому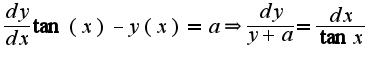 после интегрирования данного равенства, получим
после интегрирования данного равенства, получим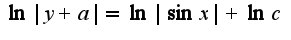 легко преобразовать последнее выражение и получить
легко преобразовать последнее выражение и получить 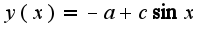 , где
, где 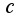 -произвольная константа
-произвольная константа
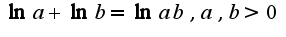 Т.е
Т.е 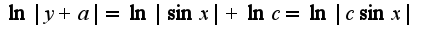 Отсюда получим, что
Отсюда получим, что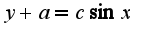 Решение второго примера аналогично, пробуйте, если не получиться, я отвечу на ваши вопросы.
Решение второго примера аналогично, пробуйте, если не получиться, я отвечу на ваши вопросы.
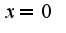 должно быть
должно быть 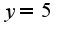 ) и найдете, что константа
) и найдете, что константа 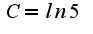 .
. 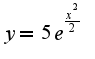
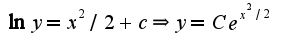 , а дальше нужно учесть начальное условие, чтобы найти произвольную константу, и как вам уже написал Анатолий, подставить в общее решение значение
, а дальше нужно учесть начальное условие, чтобы найти произвольную константу, и как вам уже написал Анатолий, подставить в общее решение значение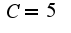 Тогда вид частного решения
Тогда вид частного решения