Поиск
| Автор | Сообщение |
|---|---|
|
Igor
#
27 дек 2006 |
|
|
Igor
#
27 дек 2006 |
|
|
О.А.
#
27 дек 2006 |
|
|
Igor
#
27 дек 2006 |
|
|
О.А.
#
27 дек 2006 |
|
|
Андрей
#
6 дек 2009 |
|
|
Андрей
#
6 дек 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
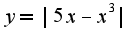 построить на отрезке от-1 до 1
построить на отрезке от-1 до 1
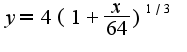 по формуле Тейлора с центром вточке
по формуле Тейлора с центром вточке 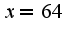 , используя разложение
, используя разложение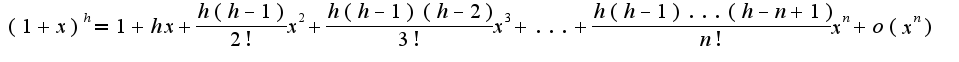 Остаточный член в форме Лагранжа можно найти в учебнике по математическому анализу.
2)производная
Остаточный член в форме Лагранжа можно найти в учебнике по математическому анализу.
2)производная 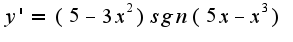 Сравнивая значения в точках
Сравнивая значения в точках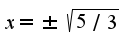 со значениями в точках
со значениями в точках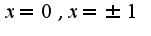 .получим, что максимальное значение функции в точке
.получим, что максимальное значение функции в точке 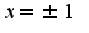 и оно равно 4
и оно равно 4