Поиск
| Автор | Сообщение |
|---|---|
|
Оксана
#
22 ноя 2009 |
|
|
О.А.
#
22 ноя 2009 |
|
|
Александра
#
28 ноя 2009 |
|
|
О.А.
#
28 ноя 2009 |
|
|
Ната
#
7 дек 2009 |
|
|
О.А.
#
7 дек 2009 |
|
|
Ната
#
7 дек 2009 |
|
|
Ната
#
7 дек 2009 |
|
|
Натали
#
7 дек 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
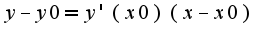
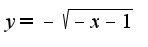 проходящей через точку с координатами (-3;0). Скажите правильно ли решение?
проходящей через точку с координатами (-3;0). Скажите правильно ли решение?
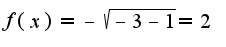
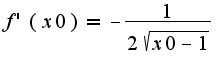
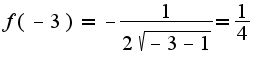
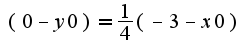
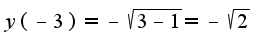 производная функции найдена неверно
производная функции найдена неверно