Поиск
| Автор | Сообщение |
|---|---|
|
Иван
#
1 апр 2009 |
|
|
О.А.
#
1 апр 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
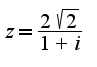
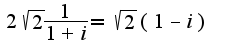 -алгебраическая форма записи
Пусть
-алгебраическая форма записи
Пусть 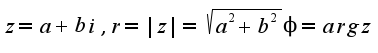 Тогда по определению аргумента имеем:
Тогда по определению аргумента имеем: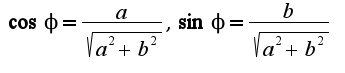 Отсюда получается
Отсюда получается
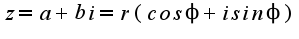 .это тригонометрическая форма записи комплексного числа
.это тригонометрическая форма записи комплексного числа