Поиск
| Автор | Сообщение |
|---|---|
|
ИринаЯ
#
7 дек 2007 |
|
|
Владимир
#
7 дек 2007 |
|
|
Владимир
#
7 дек 2007 |
|
|
ИринаЯ
#
7 дек 2007 |
|
|
О.А.
#
7 дек 2007 |
|
|
Владимир
#
7 дек 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
![$\lim_{x\to 1^+} \frac{[ln(x-1)]}{[\frac{1}{lnx}]}$ $\lim_{x\to 1^+} \frac{[ln(x-1)]}{[\frac{1}{lnx}]}$](http://teacode.com/service/latex/latex.png?latex=%5Clim_%7Bx%5Cto+1%5E%2B%7D+%5Cfrac%7B%5Bln%28x-1%29%5D%7D%7B%5B%5Cfrac%7B1%7D%7Blnx%7D%5D%7D&fontsize=21)
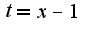 , тогда
, тогда 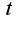 будет стремиться к
будет стремиться к 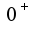
![$\lim_{x \to 1^+} ln(x) ln(x-1) => [zamena] => \lim_{t \to 0^+} ln(t+1)ln(t)$ $\lim_{x \to 1^+} ln(x) ln(x-1) => [zamena] => \lim_{t \to 0^+} ln(t+1)ln(t)$](http://teacode.com/service/latex/latex.png?latex=%5Clim_%7Bx+%5Cto+1%5E%2B%7D+ln%28x%29+ln%28x-1%29+%3D%3E+%5Bzamena%5D+%3D%3E+%5Clim_%7Bt+%5Cto+0%5E%2B%7D+ln%28t%2B1%29ln%28t%29&fontsize=21) Приводим к неопределенности вида
Приводим к неопределенности вида 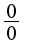
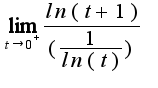 Делаем замену на ЭБМ:
Делаем замену на ЭБМ:
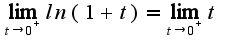
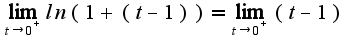 Получаем:
Получаем:
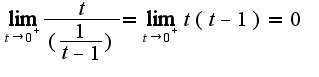
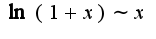 при
при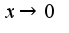 , но не справедливо асимптотическое равенство
, но не справедливо асимптотическое равенство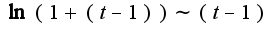 ,т.к.
,т.к.