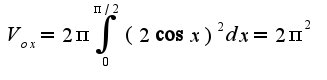Поиск
| Автор | Сообщение |
|---|---|
|
Наталья
#
23 мар 2009 |
|
|
О.А.
#
23 мар 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
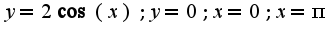 я делаю так:
я делаю так:
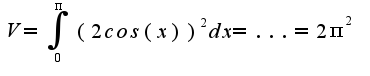 какой-то рисунок что-то странный получается, и мне кажется что интеграл составила неверно, подскажите, пожалуйста
с уважением, Наталья
какой-то рисунок что-то странный получается, и мне кажется что интеграл составила неверно, подскажите, пожалуйста
с уважением, Наталья