Поиск
| Автор | Сообщение |
|---|---|
|
Оля
#
10 янв 2007 |
|
|
О.А.
#
10 янв 2007 |
|
|
Оля
#
10 янв 2007 |
|
|
Оля
#
10 янв 2007 |
|
|
Оля
#
11 янв 2007 |
|
|
Оля
#
11 янв 2007 |
|
|
О.А.
#
12 янв 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
![$lim_{x\rightarrow+\infty}[(x^3+x^2+x+1)^{\frac{1}{3}}-\sqrt{x^2+x+1}*\frac{ln(e^x+x)}{x}]$ $lim_{x\rightarrow+\infty}[(x^3+x^2+x+1)^{\frac{1}{3}}-\sqrt{x^2+x+1}*\frac{ln(e^x+x)}{x}]$](http://teacode.com/service/latex/latex.png?latex=lim_%7Bx%5Crightarrow%2B%5Cinfty%7D%5B%28x%5E3%2Bx%5E2%2Bx%2B1%29%5E%7B%5Cfrac%7B1%7D%7B3%7D%7D-%5Csqrt%7Bx%5E2%2Bx%2B1%7D*%5Cfrac%7Bln%28e%5Ex%2Bx%29%7D%7Bx%7D%5D&fontsize=21)
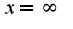 предел равен -1/6
предел равен -1/6
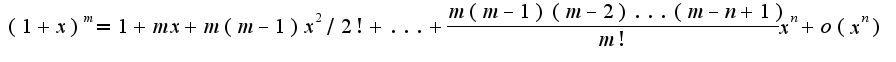 Кроме того,
Кроме того, 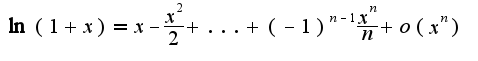 Используя вышеуказанные формулы, получим:
Используя вышеуказанные формулы, получим: