Поиск
| Автор | Сообщение |
|---|---|
|
Любаша
#
24 дек 2009 |
|
|
О.А.
#
24 дек 2009 |
|
|
Любаша
#
24 дек 2009 |
|
|
Любаша
#
24 дек 2009 |
|
|
О.А.
#
24 дек 2009 |
|
|
Любаша
#
26 дек 2009 |
|
|
Любаша
#
26 дек 2009 |
|
|
Любаша
#
26 дек 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
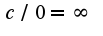 3)известен предел
3)известен предел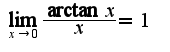 4) нужно свести ко второму замечательному пределу
4) нужно свести ко второму замечательному пределу