Поиск
| Автор | Сообщение |
|---|---|
|
willi_wi
#
16 янв 2013 |
|
|
AVM
#
17 янв 2013 |
|
|
willi_wi
#
18 янв 2013 |
|
|
o_a
#
18 янв 2013 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
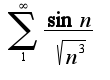 , используя признак сравнения для ряда
, используя признак сравнения для ряда 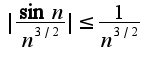 Так как ряд вида
Так как ряд вида 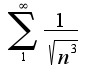 сходится,то сходится и исходный ряд
сходится,то сходится и исходный ряд
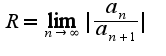 . У данного ряда
. У данного ряда 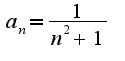 Затем область сходимости
Затем область сходимости 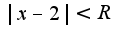 , кроме того, нужно исследовать поведение ряда на концах интервала области сходимости.
, кроме того, нужно исследовать поведение ряда на концах интервала области сходимости.