| Автор | Сообщение |
|---|---|
|
Вадим
#
20 сен 2007 |
|
|
Вадим
#
20 сен 2007 |
|
|
Евгений
#
1 окт 2007 |
|
|
О.А.
#
1 окт 2007 |
|
|
Евгений
#
1 окт 2007 |
|
|
Бодя
#
7 окт 2007 |
|
|
О.А.
#
7 окт 2007 |
|
|
Бодя
#
7 окт 2007 |
|
|
ЕЛЕНА
#
7 окт 2007 |
|
|
О.А.
#
8 окт 2007 |
|
|
ЕЛЕНА
#
8 окт 2007 |
|
|
Кветка
#
10 окт 2007 |
|
|
О.А.
#
10 окт 2007 |
|
|
Маруся
#
18 окт 2007 |
|
|
О.А.
#
18 окт 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
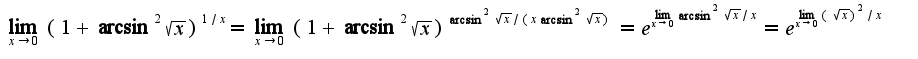 При решении использован второй замечательный предел и асимптотическое равенство
При решении использован второй замечательный предел и асимптотическое равенство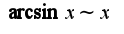 при
при 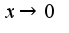
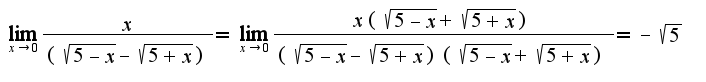 2)нужно знаменатель
2)нужно знаменатель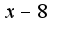 разложить как разность кубов ответ
разложить как разность кубов ответ 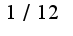
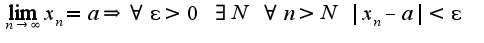 или доказать, что у данной последовательности две предельные точки
2) введите замену
или доказать, что у данной последовательности две предельные точки
2) введите замену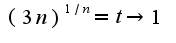 сократите дробь на множитель
сократите дробь на множитель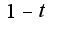 ответ 1/4
ответ 1/4