Поиск
| Автор | Сообщение |
|---|---|
|
Данила
#
26 фев 2007 |
|
|
О.А.
#
26 фев 2007 |
|
|
Данила
#
8 мар 2007 |
|
|
О.А.
#
8 мар 2007 |
|
|
Данила
#
11 мар 2007 |
|
|
Данила
#
13 мар 2007 |
|
|
О.А.
#
14 мар 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
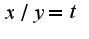
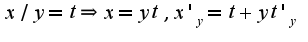
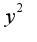 , получим:
, получим: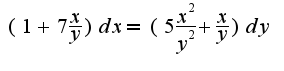 Производим замену:
Производим замену: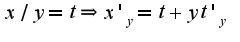 Следовательно,
Следовательно, 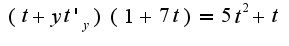 после упрощения получим
после упрощения получим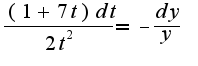 Данное уравнение-с разделенными переменными.Интегрируем:
Данное уравнение-с разделенными переменными.Интегрируем: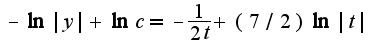 Можно потегнцировать, тогда
Можно потегнцировать, тогда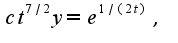 где
где