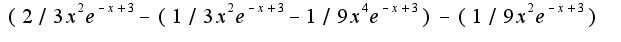Страницы: 1 2
Поиск| Автор | Сообщение |
|---|---|
|
Таня
#
16 ноя 2007 |
|
|
О.А.
#
16 ноя 2007 |
|
|
Таня
#
16 ноя 2007 |
|
|
Таня
#
16 ноя 2007 |
|
|
О.А.
#
16 ноя 2007 |
|
|
Таня
#
16 ноя 2007 |
|
|
О.А.
#
16 ноя 2007 |
|
|
Таня
#
16 ноя 2007 |
|
|
Таня
#
16 ноя 2007 |
|
|
О.А.
#
16 ноя 2007 |
|
|
Таня
#
16 ноя 2007 |
|
|
Таня
#
16 ноя 2007 |
|
|
Таня
#
16 ноя 2007 |
Страницы: 1 2
Чтобы написать сообщение, необходимо войти или зарегистрироваться
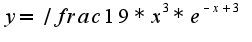
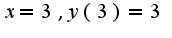 , точки перегиба
, точки перегиба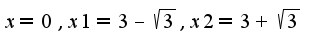 Для поиска точек экстремума привлекают первую производную, для нахождения точек перегиба-вторую производную, загляните в учебник
Для поиска точек экстремума привлекают первую производную, для нахождения точек перегиба-вторую производную, загляните в учебник
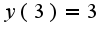 -значение функции
-значение функции 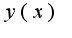 при
при 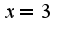
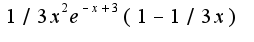 / Далее я эту производную преравняла к нулю и получила x равен:3 и плю минус корень из 1/3
/ Далее я эту производную преравняла к нулю и получила x равен:3 и плю минус корень из 1/3
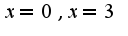 ,
, 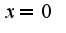 не является точкой экстремума, т.к.не происходит смены знака первой производной при переходе через эту точку
не является точкой экстремума, т.к.не происходит смены знака первой производной при переходе через эту точку