Поиск
| Автор | Сообщение |
|---|---|
|
Sonic
#
20 дек 2006 |
|
|
О.А.
#
20 дек 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
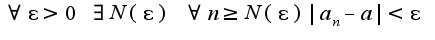 В данном примере
В данном примере 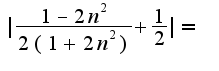
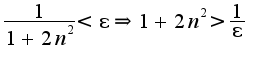
![$,\;n>\sqrt{\frac{1-\epsilon}{2\epsilon}}\rightarrow N(\epsilon)=[\sqrt{\frac{1-\epsilon}{2\epsilon}}]$ $,\;n>\sqrt{\frac{1-\epsilon}{2\epsilon}}\rightarrow N(\epsilon)=[\sqrt{\frac{1-\epsilon}{2\epsilon}}]$](http://teacode.com/service/latex/latex.png?latex=%2C%5C%3Bn%3E%5Csqrt%7B%5Cfrac%7B1-%5Cepsilon%7D%7B2%5Cepsilon%7D%7D%5Crightarrow+N%28%5Cepsilon%29%3D%5B%5Csqrt%7B%5Cfrac%7B1-%5Cepsilon%7D%7B2%5Cepsilon%7D%7D%5D&fontsize=21)