Поиск
| Автор | Сообщение |
|---|---|
|
Лиза
#
15 ноя 2006 |
|
|
О.А.
#
15 ноя 2006 |
|
|
Лиза
#
15 ноя 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
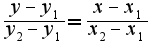 Подставляя в эту формулу координаты, получим уравнение искомой прямой :
Подставляя в эту формулу координаты, получим уравнение искомой прямой :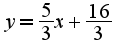 Таким образом, угловой коэффициент данной прямой равен
Таким образом, угловой коэффициент данной прямой равен 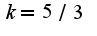 У параллельных прямых угловые коэффициенты равны, поэтому находим угловой коэффициент кривой, который равен первой производной(
У параллельных прямых угловые коэффициенты равны, поэтому находим угловой коэффициент кривой, который равен первой производной(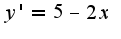 и приравниваем
и приравниваем  , получим:
, получим: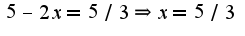 Уравнение касательной к данной кривой имеет вид:
Уравнение касательной к данной кривой имеет вид: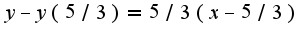 Раскрывая скобки и приводя подобные, получим:
Раскрывая скобки и приводя подобные, получим: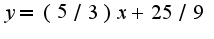 (См. графикhttp://matan.isu.ru/kons2.gif)
2)исследование нужно проводить по известной схеме:
1)область определения
(См. графикhttp://matan.isu.ru/kons2.gif)
2)исследование нужно проводить по известной схеме:
1)область определения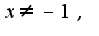 . то есть
. то есть 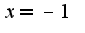 -вертикальная асимптота,
2)асимптоты
-вертикальная асимптота,
2)асимптоты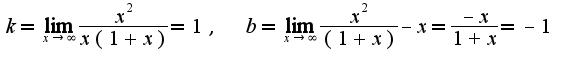 получается наклонная асимптота
получается наклонная асимптота 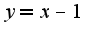 .
3)исследовать на наличие экстремуммов:
.
3)исследовать на наличие экстремуммов: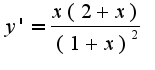 Проводя исследование то есть находя стационарные точки получим, что
Проводя исследование то есть находя стационарные точки получим, что 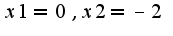 По смене знака у первой производной находим, что
По смене знака у первой производной находим, что 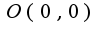 -точка минимума,A(-2,-4)-точка максимума.
4)нужно по второй производной исследовать на выпуклость и вогнутость, точек перегиба нет.
5) окончательно получаем график:http://matan.isu.ru/kons1.gif
-точка минимума,A(-2,-4)-точка максимума.
4)нужно по второй производной исследовать на выпуклость и вогнутость, точек перегиба нет.
5) окончательно получаем график:http://matan.isu.ru/kons1.gif