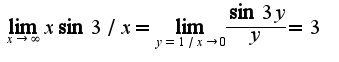Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
Поиск| Автор | Сообщение |
|---|---|
|
Маша
#
14 дек 2008 |
|
|
О.А.
#
14 дек 2008 |
|
|
Маша
#
14 дек 2008 |
|
|
О.А.
#
14 дек 2008 |
|
|
алена
#
25 дек 2008 |
|
|
О.А.
#
25 дек 2008 |
|
|
KSU
#
26 дек 2008 |
|
|
KSU
#
26 дек 2008 |
|
|
О.А.
#
26 дек 2008 |
|
|
кристина
#
4 янв 2009 |
|
|
О.А.
#
4 янв 2009 |
|
|
Алекса
#
8 янв 2009 |
|
|
О.А.
#
9 янв 2009 |
|
|
крис
#
17 янв 2009 |
|
|
Ноль
#
17 янв 2009 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
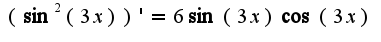
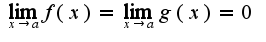 , а также если обе являются дифференцируемыми в некоторой проколотой окрестности точки a, причем
, а также если обе являются дифференцируемыми в некоторой проколотой окрестности точки a, причем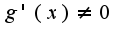 в проколотой окрестности точки a, и если существует предел отношения производных, то существует предел отношения функций, справедливо равенство
в проколотой окрестности точки a, и если существует предел отношения производных, то существует предел отношения функций, справедливо равенство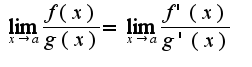
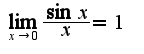 для данного примера предварительно сделать замену переменной
для данного примера предварительно сделать замену переменной