Поиск
| Автор | Сообщение |
|---|---|
|
Матрена
#
18 ноя 2007 |
|
|
Анатолий
#
18 ноя 2007 |
|
|
Матрена
#
18 ноя 2007 |
|
|
Матрена
#
18 ноя 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
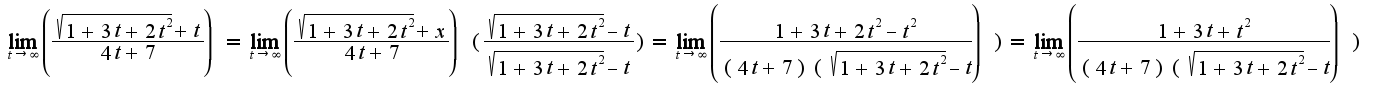 Опять бесконечность на бесконечность неопределенность.
Может, надо выделить полные квадраты?
Прям не знаю.
Опять бесконечность на бесконечность неопределенность.
Может, надо выделить полные квадраты?
Прям не знаю.
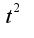
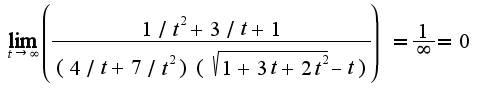 Но все равно ответ неправильный. Должно быть
Но все равно ответ неправильный. Должно быть 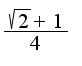 Я уж и по правилу Лопиталя пробовала - тоже не то.
После всех преобразований по правилу Лопиталя получила вот что:
Я уж и по правилу Лопиталя пробовала - тоже не то.
После всех преобразований по правилу Лопиталя получила вот что:
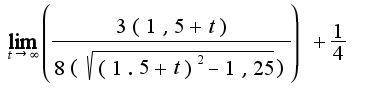 Здесь уже поближе к правде: появилась 1/4, но что делать с первым слагаемым - не знаю.
Здесь уже поближе к правде: появилась 1/4, но что делать с первым слагаемым - не знаю.