Поиск
| Автор | Сообщение |
|---|---|
|
Fedya
#
4 дек 2007 |
|
|
О.А.
#
4 дек 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
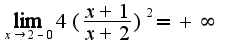 ,
,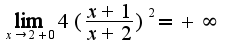 точка
точка 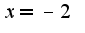 -разрыв второго рода, т.к. не существует конечных лево и правосторонних пределов, никакого противоречия с графиком функции нет
-разрыв второго рода, т.к. не существует конечных лево и правосторонних пределов, никакого противоречия с графиком функции нет