Поиск
| Автор | Сообщение |
|---|---|
|
Эвелина
#
14 ноя 2007 |
|
|
О.А.
#
14 ноя 2007 |
|
|
Эвелина
#
15 ноя 2007 |
|
|
О.А.
#
15 ноя 2007 |
|
|
Эвелина
#
15 ноя 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
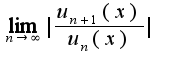 , где
, где 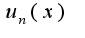 - общий член данного ряда. Полученное выражение должно быть меньше единицы, кроме того исследуйте ряд на сходимость на концах интервала
- общий член данного ряда. Полученное выражение должно быть меньше единицы, кроме того исследуйте ряд на сходимость на концах интервала