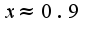| Автор | Сообщение |
|---|---|
|
Екатерина
#
4 апр 2009 |
|
|
Екатерина
#
4 апр 2009 |
|
|
О.А.
#
4 апр 2009 |
|
|
Лена
#
7 апр 2009 |
|
|
О.А.
#
7 апр 2009 |
|
|
Лена
#
7 апр 2009 |
|
|
О.А.
#
7 апр 2009 |
|
|
Анна
#
8 апр 2009 |
|
|
О.А.
#
8 апр 2009 |
|
|
Анна
#
8 апр 2009 |
|
|
О.А.
#
8 апр 2009 |
|
|
Анна
#
8 апр 2009 |
|
|
О.А.
#
8 апр 2009 |
|
|
Анна
#
8 апр 2009 |
|
|
О.А.
#
8 апр 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
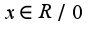 из вида второй производной следует, что при
из вида второй производной следует, что при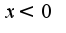 функция имеет выпуклость вниз, при
функция имеет выпуклость вниз, при 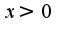 -выпуклость вверх, кроме того есть наклонная асимптота
-выпуклость вверх, кроме того есть наклонная асимптота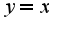
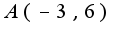 вторая производная найдена неверно
вторая производная найдена неверно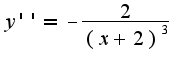 график функции выпуклый вверх при
график функции выпуклый вверх при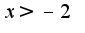 и выпуклый вниз при
и выпуклый вниз при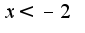 точек перегиба нет, остальное правильно решено
точек перегиба нет, остальное правильно решено
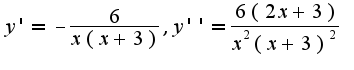
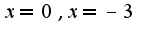 если учитывать область определения, то функция везде убывает, нет локальных экстремумов, нет точек перегиба, если
если учитывать область определения, то функция везде убывает, нет локальных экстремумов, нет точек перегиба, если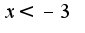 то график имеет выпуклость вверх, если
то график имеет выпуклость вверх, если