Поиск
| Автор | Сообщение |
|---|---|
|
васька
#
13 сен 2011 |
|
|
o_a
#
13 сен 2011 |
|
|
Ню)
#
11 окт 2011 |
|
|
o_a
#
11 окт 2011 |
|
|
paulinio
#
30 окт 2011 |
|
|
o_a
#
30 окт 2011 |
|
|
paulinio
#
30 окт 2011 |
|
|
o_a
#
30 окт 2011 |
|
|
paulinio
#
16 ноя 2011 |
|
|
o_a
#
16 ноя 2011 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
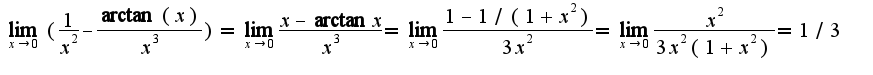
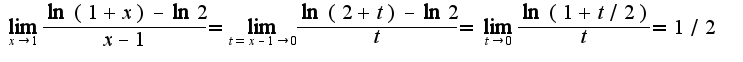
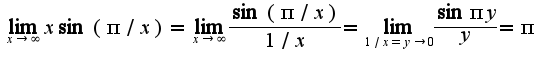
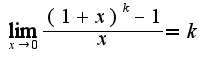 , то нужно произвести замену
, то нужно произвести замену 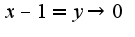 , во втором примере, соответственно,
, во втором примере, соответственно,