Поиск
| Автор | Сообщение |
|---|---|
|
Антон
#
21 июн 2007 |
|
|
Антон
#
22 июн 2007 |
|
|
О.А.
#
22 июн 2007 |
|
|
Антон
#
22 июн 2007 |
|
|
О.А.
#
22 июн 2007 |
|
|
Антон
#
22 июн 2007 |
|
|
Антон
#
22 июн 2007 |
|
|
О.А.
#
22 июн 2007 |
|
|
Антон
#
23 июн 2007 |
|
|
Антон
#
23 июн 2007 |
|
|
Антон
#
23 июн 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
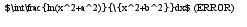 интеграл от 0 до + бесконечности. b<>0 (не равно нулю) - фиксировано. a - параметр.
Задание:
1) при каких "а" интеграл сходится
2) при каких "а" дифф-ся
3) при каких "а" непрерывно дифф-ся
4) вычислить f'(a)
Чем сможете, помогите, пожалуйста
интеграл от 0 до + бесконечности. b<>0 (не равно нулю) - фиксировано. a - параметр.
Задание:
1) при каких "а" интеграл сходится
2) при каких "а" дифф-ся
3) при каких "а" непрерывно дифф-ся
4) вычислить f'(a)
Чем сможете, помогите, пожалуйста
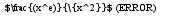 здесь я заменил логарифм на х в любой степени, это не ошибка? если можно, cледовательно интеграл сходится при любых а
при х--> 0
здесь я заменил логарифм на х в любой степени, это не ошибка? если можно, cледовательно интеграл сходится при любых а
при х--> 0 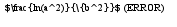 cледовательно сх-ся при любых а и вообще точка 0 не является особой
Как показать что f(a) дифф-ма?
дифф-ма, т.к. существует конечный придел? Т.е. по определению? Можно как-нибудь проще?
А чтобы показать, что она непрерывно дифф-ма покажем что производная этой функции сх-ся.
Так правильно?
f'(a)=
cледовательно сх-ся при любых а и вообще точка 0 не является особой
Как показать что f(a) дифф-ма?
дифф-ма, т.к. существует конечный придел? Т.е. по определению? Можно как-нибудь проще?
А чтобы показать, что она непрерывно дифф-ма покажем что производная этой функции сх-ся.
Так правильно?
f'(a)=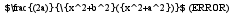 так я нашёл производную функции f(a). Вопрос такой, я правильно взял производную по a или нужно было брать по x?
при x--> бесконечности
так я нашёл производную функции f(a). Вопрос такой, я правильно взял производную по a или нужно было брать по x?
при x--> бесконечности 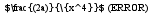 сх-ся при любом а
при х--> 0
сх-ся при любом а
при х--> 0 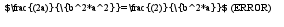 при a<>0 (не равно 0) сх-ся
Ещё раз прошу помочь хоть чем-нибудь, пожалуйста
при a<>0 (не равно 0) сх-ся
Ещё раз прошу помочь хоть чем-нибудь, пожалуйста
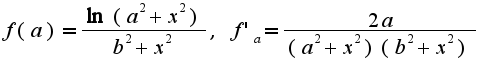 -непрерывны при
-непрерывны при 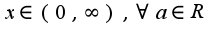 Инеграл равномерно сходится на основании признака Вейерштрасса на любом сегменте
Инеграл равномерно сходится на основании признака Вейерштрасса на любом сегменте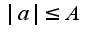 ,т.к.
,т.к. 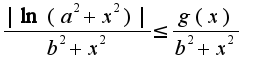 , где
, где 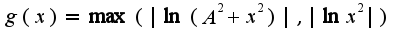
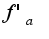 тоже равномерно сходится при
тоже равномерно сходится при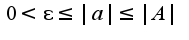 Чтобы вычислить
Чтобы вычислить 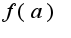 надо проинтегрировать
надо проинтегрировать 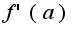 по переменной
по переменной  , получим
, получим 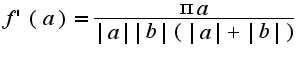 Из этого равенства надо найти
Из этого равенства надо найти 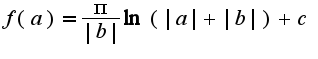 Произвольная константа находится из данного интеграла
Произвольная константа находится из данного интеграла 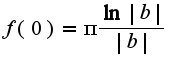 Сл-но,
Сл-но, 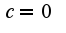
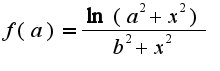 дифф-ма и непрерывно дифф-ма и при каких значениях "а"
или хотя бы какое условие должно выполняться чтобы показать что функция дифф-ма и соотвтественно непрерывно дифф-ма?
дифф-ма и непрерывно дифф-ма и при каких значениях "а"
или хотя бы какое условие должно выполняться чтобы показать что функция дифф-ма и соотвтественно непрерывно дифф-ма?
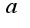 , используйте признак Вейерштрасса
, используйте признак Вейерштрасса
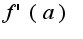 по переменной
по переменной 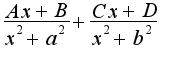 , затем проинтегрировать, интегралы табличные(первообразные равны
, затем проинтегрировать, интегралы табличные(первообразные равны  )
)
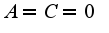
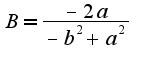
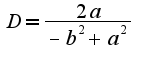 затем проинтегрировал и получилось
затем проинтегрировал и получилось 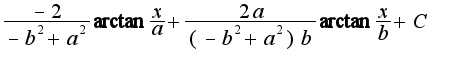 но как привести к виду
но как привести к виду 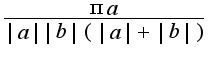 ???
???
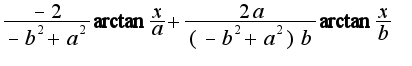 Подставим
Подставим 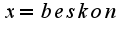 и вычтем
и вычтем 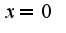 т.к.
т.к. 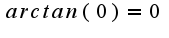 , а
, а 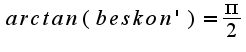 получим
получим 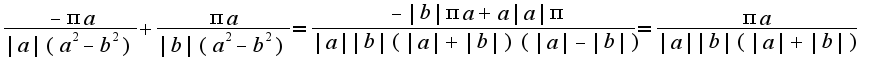 Но откуда в первой дроби
Но откуда в первой дроби 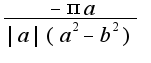 в числители взяли
в числители взяли 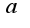 ?
?
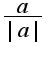 и соответственно с b тоже самое.
Ещё раз СПАСИБО!!!
и соответственно с b тоже самое.
Ещё раз СПАСИБО!!!