Форумы > Консультация по матанализу > Решение пределов по правилу Лопиталя

Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

Поиск
Автор Сообщение
daria_nik #
29 мар 2011
Здравствуйте, не могли бы Вы мне помочь? Найти предел, используя правило лопиталя при x стремится к бесконечности. e^x / 2x-3 я нахожу производные числителя и знаменателя и получается e^x / -3x^2 и делаю вывод, что и числитель и знаменатель стремятся к ?бесконечности?, и ответ бесконечность?(вот на этом месте у меня проблема, я понимаю, что когда x стремится к какому-то числу, надо это число подставить на место x и вычислить ответ, но запуталась, что надо делать если x стремится к бесконечности как в этом так и в других примерах, может быть есть свод правил на эту тему? в каких случаях числитель/знаменатель стремится к нулю, а в каких к бесконечности? и какой в этих случаях ответ?) спасибо огромное
o_a #
29 мар 2011
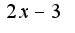Здравствуйте. Если в знаменателе данной дроби стоит функция $2x-3$,то производная от нее равна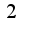$2$откуда получилось 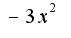$-3x^2$?Нахождение пределов по правилу Лопиталя хорошо освящено в любом учебнике по математическому анализу или высшей математике $\lim_{x\rightarrow +\infty}\frac{e^{x}}{2x-3}=\lim_{x\rightarrow +\infty}\frac{e^{x}}{2}=+\infty$$\lim_{x\rightarrow -\infty}\frac{e^{x}}{2x-3}=\lim_{x\rightarrow -\infty}\frac{e^{x}}{2}=0$
Студентка #
23 окт 2011
Здравствуйте. Помогите пожалуйста с примером: lim(1+3tg^2x)^ctg^2x, стремится к нулю
o_a #
20 апр 2011
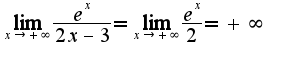
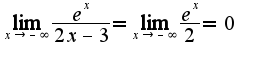
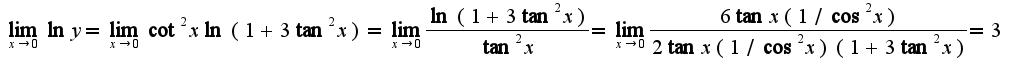здравствуйте. Чтобы можно было непосредственно использовать правило Лопиталя, нужно предварительно прологарифмировать выражение, затем перейти к пределу$\lim_{x\rightarrow 0} \ln y=\lim_{x\rightarrow 0}\cot^2 x\ln(1+3\tan^2 x)=\lim_{x\rightarrow 0}\frac{\ln(1+3\tan^2 x)}{\tan^2 x}=\lim_{x\rightarrow 0}\frac{6\tan x (1/\cos^2 x)}{2\tan x(1/\cos^2 x)(1+3\tan^2 x)}=3$Таким образом из равенства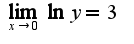$\lim_{x\rightarrow 0}\ln y=3$получим, что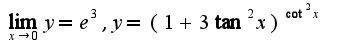$\lim_{x\rightarrow 0}y=e^3,y=(1+3\tan^2 x)^{\cot^2 x}$
Студентка #
20 апр 2011
Спасибо большое!
мучающийся студента #
5 июн 2011
Пожалуйста, помогите: (cos*ln*x*(x-3))/(ln*(e^x-e^3)) стремится к 3+0
Тусенька #
сегодня в 18:49
подскажите, не могу решить: раскрыть неопределенность с помощью правила Лопиталя: lim √6-x - √x-2 x→4 √5-x - √x-3
o_a #
30 ноя 2011
по правилу Лопиталя сначала надо найти производные от числителя и знаменателя, затем подставить предельную точку$\lim_{x\rightarrow 4}\frac{\sqrt{6-x}-\sqrt{x-2}}{\sqrt{5-x}-\sqrt{x-3}}=\lim_{x\rightarrow 4}\frac{(-1/2\sqrt{6-x})-1/2\sqrt{x-2}}{(-1/2\sqrt{5-x})-1/2\sqrt{x-2}}=1/\sqrt{2}$
Тусенька #
30 ноя 2011
раскрыть неопределенность с помощью правила Лопиталя: lim (x+1)^(x+2) x→∞ (x-2)^(x+2)
o_a #
15 окт 2008
а вы абсолютно неправильно поняли, что я за вас буду решать задачи. Давайте учебник изучайте, нельзя так превратно понимать цель данной консультации
Тусенька #
30 ноя 2011
Вы извините, но я не прошу решать мне эту задачу, я только не могу понять как найти производную например от (x+1)^(x+2).А дальше решить сама я смогу. я же не прошу мне полностью писать решение данной задачи, я думаю вы мне просто напишите то,от чего можно оттолкнуться в решении,вот и все.
o_a #
30 ноя 2011
решение подобных примеров(нахождение производных от показательно степенной функции) доступно изложено в сборнике задач по математическому анализу часть 1 под редакцией Л.Д. Кудрявцева
Тусенька #
30 ноя 2011
спасибо.все-таки вы зря думаете,что я просила вас чтобы вы за меня все решали, я действительно хотела проконсультироваться по тем заданиям, в которых мне что-либо не понятно.Просто я учусь на первом курсе заочном отделении и у меня есть много вопросов,которые мне не понятны.Думала что ваши консультации мне помогут,но если вы не так поняли меня,то извините.Но все равно спасибо.
Глеб #
12 дек 2011
Время доброе!Прошу помочь с решением трех примеров 1)x->1 Lim(1-sin^2((пи*x)/2)))/(x-1)^2 2)x->∞ Lim(x-x^2*ln(1+1/x)) 3)x->0 Lim(x+e^2x)^(1/x)
o_a #
12 дек 2011
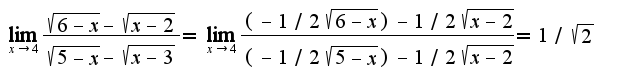
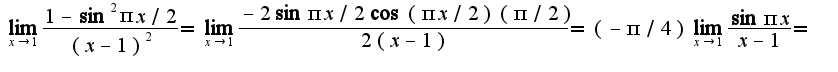
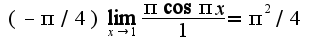добрый день, если использовать правило Лопиталя, то в примере N1 оно применяется непосредственно два раза: 1)$\lim_{x\rightarrow 1}\frac{1-\sin^2 \pi x/2}{(x-1)^2}=\lim_{x\rightarrow 1}\frac{-2\sin \pi x/2\cos (\pi x/2)(\pi /2)}{2(x-1)}=(-\pi/4)\lim_{x\rightarrow 1}\frac{\sin \pi x}{x-1}=$$(-\pi /4)\lim_{x\rightarrow 1}\frac{\pi \cos \pi x}{1}=\pi^2/4$ 2) предварительно преобразовать: выражение представить неопределенность вида 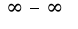$\infty-\infty$в виде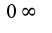$0\infty$ 3)сначала прологарифмировать выражение, затем находить предел, подобные примеры решены в сборнике задач по математическому анализу под редакцией Кудрявцева Л.Д.

Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

Форумы > Консультация по матанализу > Решение пределов по правилу Лопиталя
Чтобы написать сообщение, необходимо войти или зарегистрироваться

© teacode.com, 2004-2016