Поиск
| Автор | Сообщение |
|---|---|
|
Luda
#
16 дек 2012 |
|
|
o_a
#
16 дек 2012 |
|
|
Luda
#
16 дек 2012 |
|
|
o_a
#
16 дек 2012 |
|
|
Luda
#
17 дек 2012 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
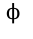 найдены неверно. Рекомендую сначала построить область D, тогда легко найдете пределы. Ясно , что пределы по
найдены неверно. Рекомендую сначала построить область D, тогда легко найдете пределы. Ясно , что пределы по 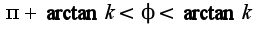 . Данные пределы получены решением неравенства
. Данные пределы получены решением неравенства 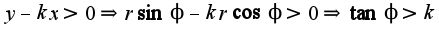
 или можно поставить перед интегралом минус, тогда поменять пределы, так как справедливо свойство интеграла
или можно поставить перед интегралом минус, тогда поменять пределы, так как справедливо свойство интеграла