Поиск
| Автор | Сообщение |
|---|---|
|
Коваль Иван
#
29 мая 2008 |
|
|
О.А.
#
29 мая 2008 |
|
|
Коваль Иван
#
29 мая 2008 |
|
|
О.А.
#
29 мая 2008 |
|
|
Коваль Иван
#
30 мая 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
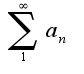 . что для всех
. что для всех 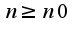 и для всех
и для всех 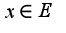 выполняется неравенство
выполняется неравенство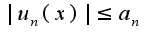 , то исходный ряд сходится абсолютно и равномерно. Для данного ряда очевидно неравенство
, то исходный ряд сходится абсолютно и равномерно. Для данного ряда очевидно неравенство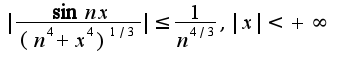 А т.к. числовой ряд
А т.к. числовой ряд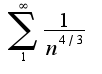 сходится, то по признаку Вейерштрасса сходится и исходный ряд абсолютно и равномерно
сходится, то по признаку Вейерштрасса сходится и исходный ряд абсолютно и равномерно