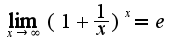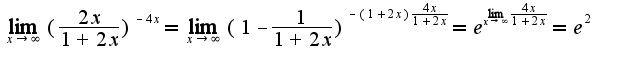Поиск
| Автор | Сообщение |
|---|---|
|
Игорь
#
18 дек 2006 |
|
|
О.А.
#
18 дек 2006 |
|
|
Игорь
#
19 дек 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
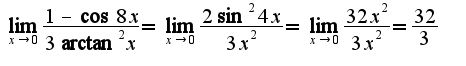 Использованы асимптотические равенства
Использованы асимптотические равенства при
при 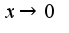 2) решается непосредственно подстановкой предельной точки
3)Надо использовать второй замечательный предел
2) решается непосредственно подстановкой предельной точки
3)Надо использовать второй замечательный предел