Поиск
| Автор | Сообщение |
|---|---|
|
svtmtvtn
#
22 окт 2016 |
|
|
o_a
#
22 окт 2016 |
|
|
svtmtvtn
#
23 окт 2016 |
|
|
o_a
#
23 окт 2016 |
|
|
svtmtvtn
#
23 окт 2016 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
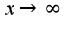 , то нужно преобразовать выражение и использовать асимптотическое равенство
, то нужно преобразовать выражение и использовать асимптотическое равенство 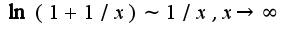 Можно использовать разложение по формуле Маклорена подпредельной функции, ответ 1/8
Можно использовать разложение по формуле Маклорена подпредельной функции, ответ 1/8
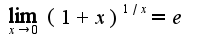 Достаточно представить выражение в виде
Достаточно представить выражение в виде 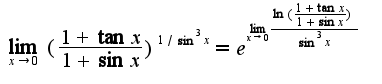 Затем использовать асимптотические равенства
Затем использовать асимптотические равенства 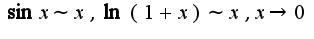 В третьем примере нужно преобразовать выражение:
В третьем примере нужно преобразовать выражение: 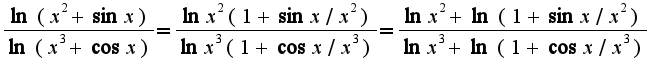 и перейти к пределу. Ответ:2/3
В четвертом примере сначала преобразовать выражение, применяя формулу тангенс суммы углов, затем использовать асимптотическую формулу
и перейти к пределу. Ответ:2/3
В четвертом примере сначала преобразовать выражение, применяя формулу тангенс суммы углов, затем использовать асимптотическую формулу 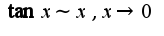 Ответы:
Ответы: