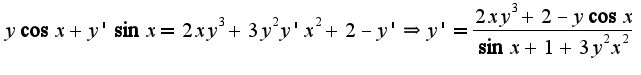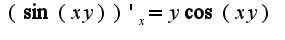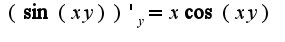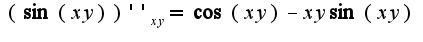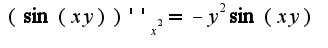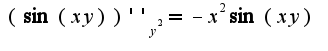Поиск
| Автор | Сообщение |
|---|---|
|
Ира
#
10 окт 2006 |
|
|
О.А.
#
10 окт 2006 |
|
|
Ира
#
10 окт 2006 |
|
|
О.А.
#
10 окт 2006 |
|
|
Ира
#
10 окт 2006 |
|
|
Натали
#
31 авг 2007 |
|
|
О.А.
#
1 сен 2007 |
|
|
Натали
#
3 сен 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться

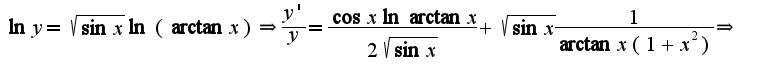
 2)из написанного условия не ясно, какой аргумент у функции
2)из написанного условия не ясно, какой аргумент у функции 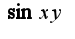 или
или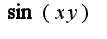 ?
?