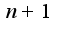Поиск
| Автор | Сообщение |
|---|---|
|
Люба
#
3 июн 2008 |
|
|
О.А.
#
3 июн 2008 |
|
|
Люба
#
4 июн 2008 |
|
|
О.А.
#
4 июн 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
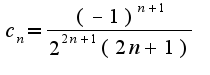 модули
модули 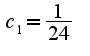 ,
,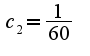 ,
,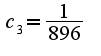 c1>c2>c3>...
c1>c2>c3>...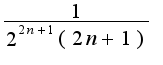
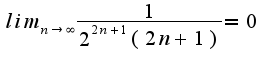 значит ряд абсолютно сходящийся
значит ряд абсолютно сходящийся
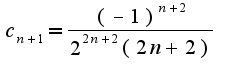
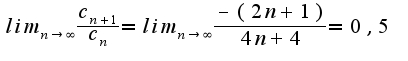 ряд абс. сходящийся
ряд абс. сходящийся
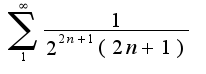 и его исследовать можно с помощью признака Даламбера, т.е. найти предел отношения последующего члена к предыдущему, есл и этот предел меньше 1, то ряд сходится:
и его исследовать можно с помощью признака Даламбера, т.е. найти предел отношения последующего члена к предыдущему, есл и этот предел меньше 1, то ряд сходится: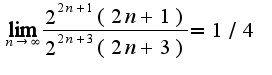 То есть ряд сходится, поэтому исходный ряд сходится абсолютно
То есть ряд сходится, поэтому исходный ряд сходится абсолютно
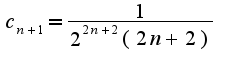
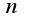 надо в формулу подставить
надо в формулу подставить