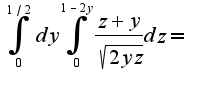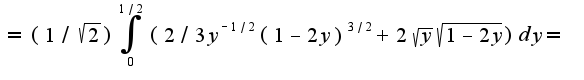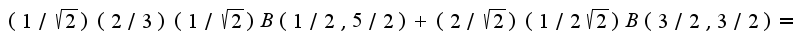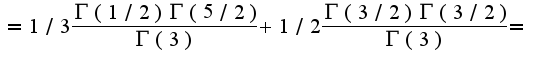Поиск
| Автор | Сообщение |
|---|---|
|
Student
#
21 мая 2005 |
|
|
О.А.
#
21 мая 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
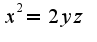 , найти площадь этой поверхности, ограниченной плоскостями: y=0, z=0,
, найти площадь этой поверхности, ограниченной плоскостями: y=0, z=0, 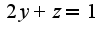 .
Помогите дибилу, спасайте идиота:))
.
Помогите дибилу, спасайте идиота:))
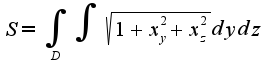 Находим
Находим 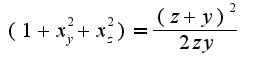 Т.к.
Т.к. 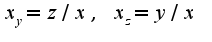 Учитывая уравнения плоскостей имеем пределы:
Учитывая уравнения плоскостей имеем пределы: