Страницы: 1 2 3 4 5 6 7 8 9 10 11
Поиск| Автор | Сообщение |
|---|---|
|
Neuch
#
24 июн 2005 |
|
|
О.А.
#
24 июн 2005 |
|
|
SpY
#
22 ноя 2005 |
|
|
О.А.
#
22 ноя 2005 |
|
|
SpY
#
24 ноя 2005 |
|
|
Mx
#
14 мая 2006 |
|
|
Александр
#
13 июн 2006 |
|
|
О.А.
#
14 июн 2006 |
|
|
О.А.
#
14 июн 2006 |
|
|
Александр
#
16 июн 2006 |
|
|
Александр
#
16 июн 2006 |
|
|
ната
#
16 июн 2006 |
|
|
Александр
#
17 июн 2006 |
|
|
О.А.
#
17 июн 2006 |
|
|
Grifon
#
11 дек 2006 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11
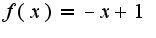 в ряд по синусам на
в ряд по синусам на 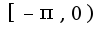 . Жду до завтрашнего вечера. Огромное спасибо!
. Жду до завтрашнего вечера. Огромное спасибо!
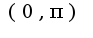 , тогда
, тогда 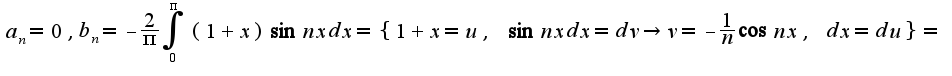
![$=-\frac{2}{\pi}[(1+x)(-\frac{1}{n}\cos nx)|_{0}^{\pi}+\frac{1}{n}\int_{0}^{\pi}\cos nxdx]=-\frac{2}{\pi n}[(1+\pi)(-1)^{n+1}+1]=\{\frac{2}{n},n=2k,-\frac{2(2+\pi)}{\pi n},n=2k-1$ $=-\frac{2}{\pi}[(1+x)(-\frac{1}{n}\cos nx)|_{0}^{\pi}+\frac{1}{n}\int_{0}^{\pi}\cos nxdx]=-\frac{2}{\pi n}[(1+\pi)(-1)^{n+1}+1]=\{\frac{2}{n},n=2k,-\frac{2(2+\pi)}{\pi n},n=2k-1$](http://teacode.com/service/latex/latex.png?latex=%3D-%5Cfrac%7B2%7D%7B%5Cpi%7D%5B%281%2Bx%29%28-%5Cfrac%7B1%7D%7Bn%7D%5Ccos+nx%29%7C_%7B0%7D%5E%7B%5Cpi%7D%2B%5Cfrac%7B1%7D%7Bn%7D%5Cint_%7B0%7D%5E%7B%5Cpi%7D%5Ccos+nxdx%5D%3D-%5Cfrac%7B2%7D%7B%5Cpi+n%7D%5B%281%2B%5Cpi%29%28-1%29%5E%7Bn%2B1%7D%2B1%5D%3D%5C%7B%5Cfrac%7B2%7D%7Bn%7D%2Cn%3D2k%2C-%5Cfrac%7B2%282%2B%5Cpi%29%7D%7B%5Cpi+n%7D%2Cn%3D2k-1&fontsize=21) Поэтому разложение имеет вид
Поэтому разложение имеет вид
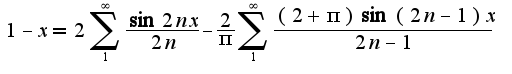
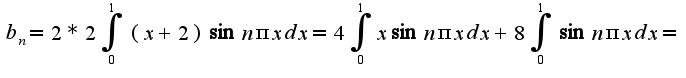
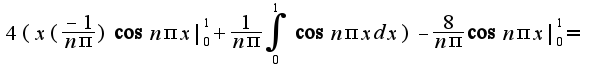
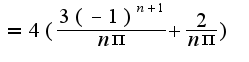 Ряд Фурье имеет вид
Ряд Фурье имеет вид 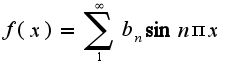 Аналогично раскладывается данная функция и по
Аналогично раскладывается данная функция и по 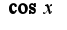 , только надо посчитать коэффициенты
, только надо посчитать коэффициенты 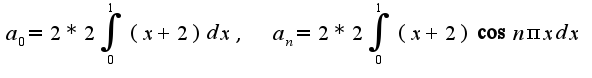 В этом случае ряд Фурье:
В этом случае ряд Фурье: 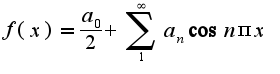
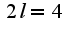 , т.е
, т.е 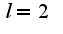 , сл-но,
, сл-но, 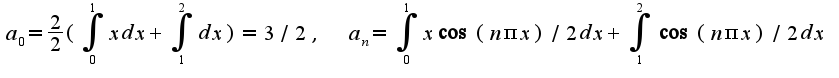 Первый интеграл берется по частям, как это делается можно посмотреть в предыдущем примере. Легко найти первообразную,
Первый интеграл берется по частям, как это делается можно посмотреть в предыдущем примере. Легко найти первообразную, 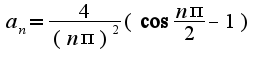
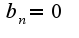 Может надо разложить
Может надо разложить 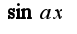 ?
?
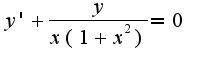 Данное уравнение -с разделяющимися переменными:
Данное уравнение -с разделяющимися переменными: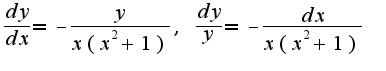
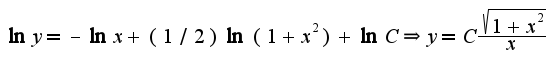 2)Затем используют метод вариации произвольной константы C,т.е. подставляют в уравнение найденное решение, считая, что C(x)зависит от x.Легко найти
2)Затем используют метод вариации произвольной константы C,т.е. подставляют в уравнение найденное решение, считая, что C(x)зависит от x.Легко найти