Поиск
| Автор | Сообщение |
|---|---|
|
Lenin
#
3 апр 2005 |
|
|
О.А.
#
3 апр 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
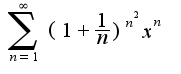
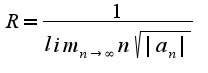 Тогда область сходимости определяется неравенством:
Тогда область сходимости определяется неравенством: 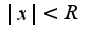 . Для данного примера
. Для данного примера 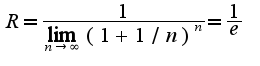 .Следовательно, область сходимости
.Следовательно, область сходимости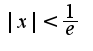 . Исследуем поведение ряда на концах отрезка, т.е. при
. Исследуем поведение ряда на концах отрезка, т.е. при 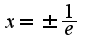 Подставим значение
Подставим значение 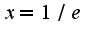 в ряд. Получим ряд
в ряд. Получим ряд 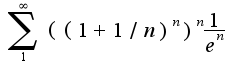 .Общий член данного ряда
.Общий член данного ряда 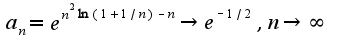 Следовательно, ряд расходится, так же как и ряд
Следовательно, ряд расходится, так же как и ряд 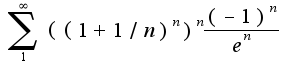 .Поэтому область сходимости исходного ряда
.Поэтому область сходимости исходного ряда