Поиск
| Автор | Сообщение |
|---|---|
|
Дарья
#
8 янв 2010 |
|
|
О.А.
#
8 янв 2010 |
|
|
Student
#
8 янв 2010 |
|
|
О.А.
#
8 янв 2010 |
|
|
Дарья
#
8 янв 2010 |
|
|
О.А.
#
8 янв 2010 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
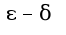 , в этом определении нужно установить зависимость
, в этом определении нужно установить зависимость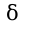 от
от 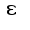 (чему равна
(чему равна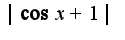 как разность косинусов
как разность косинусов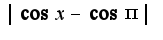
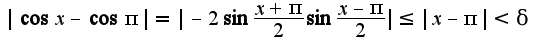
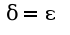 , вы все таки разберитесь с определением
, вы все таки разберитесь с определением