| Автор | Сообщение |
|---|---|
|
О.А.
#
20 мар 2005 |
|
|
Ольга Шабалина
#
20 мар 2005 |
|
|
Марченкова Анастасия
#
21 мар 2005 |
|
|
О.А.
#
21 мар 2005 |
|
|
anonim
#
1 апр 2005 |
|
|
О.А.
#
1 апр 2005 |
|
|
Алексей
#
3 апр 2005 |
|
|
О.А.
#
3 апр 2005 |
|
|
student
#
15 апр 2005 |
|
|
О.А.
#
15 апр 2005 |
|
|
studentka
#
26 апр 2005 |
|
|
О.А.
#
27 апр 2005 |
|
|
studentka
#
27 апр 2005 |
|
|
studentka
#
27 апр 2005 |
|
|
Станислав Матвеев
#
3 мая 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
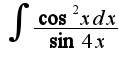 ) и нерешен N3. У Насти-3--(решено три примера)
) и нерешен N3. У Насти-3--(решено три примера)
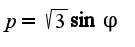 ,
, 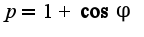 Спасибо.
Спасибо.
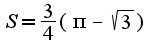
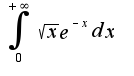 ?
?
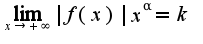 при
при 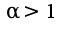 , то интеграл от
, то интеграл от 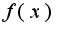 сходится. Действительно,
сходится. Действительно, 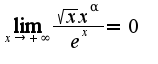 при
при 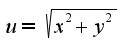 ,
, 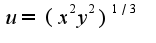 в точке О(0,0) и как их искать?
в точке О(0,0) и как их искать?
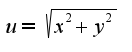 , нужно использовать определение
, нужно использовать определение 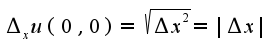 Однако, предела функции
Однако, предела функции 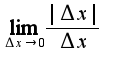 не существует. Аналогично, предела
не существует. Аналогично, предела 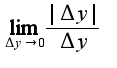 не существует. Поэтому данная функция не дифференцируема в т. O(0,0). Для функции
не существует. Поэтому данная функция не дифференцируема в т. O(0,0). Для функции 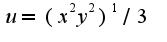 частные производные равны нулю. Здесь для нахождения частных производных также используется определение
частные производные равны нулю. Здесь для нахождения частных производных также используется определение 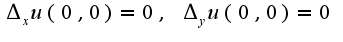 Поэтому осталось проверить выполнение условия
Поэтому осталось проверить выполнение условия 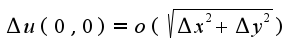 Для нахождения предела можно использовать переход в полярную систему координат. Функция является дифференцируемой в т.O(0,0).
Для нахождения предела можно использовать переход в полярную систему координат. Функция является дифференцируемой в т.O(0,0).