Поиск
| Автор | Сообщение |
|---|---|
|
SrPomidoro
#
22 окт 2014 |
|
|
o_a
#
22 окт 2014 |
|
|
SrPomidoro
#
22 окт 2014 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
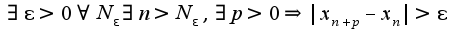 Для данного примера:
Для данного примера: 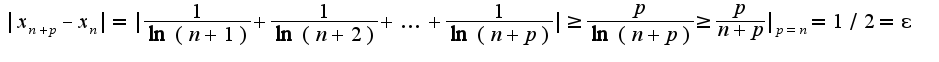 Выбирая
Выбирая 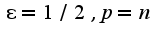 , получим, что последовательность не является фундаментальной, поэтому по критерию Коши она расходится.
, получим, что последовательность не является фундаментальной, поэтому по критерию Коши она расходится.