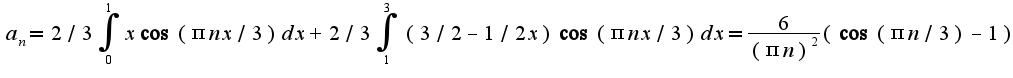Поиск
| Автор | Сообщение |
|---|---|
|
Koshi
#
17 мая 2005 |
|
|
О.А.
#
18 мая 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
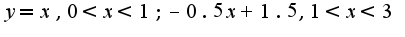 разложить в ряд по sin, затем по cos и, наконец, в тригонометрический ряд. Если можно - умоляю, напишите как. Заранее огромное спасибо:)
Если много формул - пришлите на ящик в другом формате abel85@mail.ru
разложить в ряд по sin, затем по cos и, наконец, в тригонометрический ряд. Если можно - умоляю, напишите как. Заранее огромное спасибо:)
Если много формул - пришлите на ящик в другом формате abel85@mail.ru
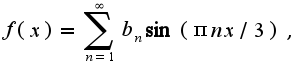 где
где 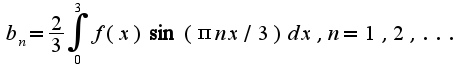 Т.е.
Т.е. 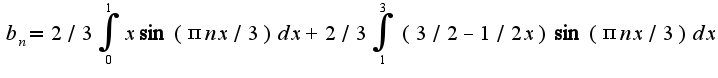 Данные интегралы легко вычислить по частям,полагая
Данные интегралы легко вычислить по частям,полагая 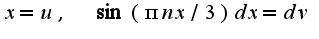 и, соответственно, во втором интеграле
и, соответственно, во втором интеграле 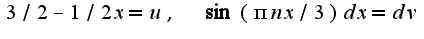 Вычисляя, получим, что
Вычисляя, получим, что 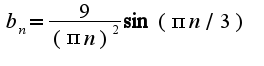 Чтобы разложить по cosx, надо продолжить данную функцию на отрезок(-3,0) четным образом. При этом,
Чтобы разложить по cosx, надо продолжить данную функцию на отрезок(-3,0) четным образом. При этом, 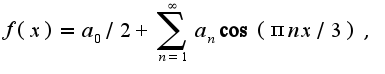 где
где 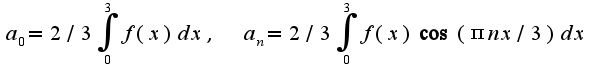 Подробное вычисление дает,
Подробное вычисление дает, 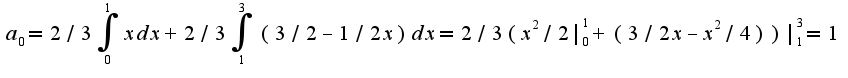 Аналогично,
Аналогично,