Поиск
| Автор | Сообщение |
|---|---|
|
Артур
#
21 янв 2007 |
|
|
О.А.
#
21 янв 2007 |
|
|
Артур
#
21 янв 2007 |
|
|
О.А.
#
21 янв 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
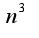
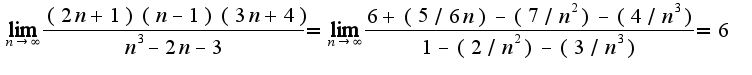 ,т.к.
,т.к.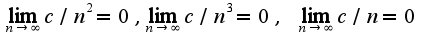 2)Нужно найти предел слева и справа в точке
2)Нужно найти предел слева и справа в точке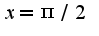 ,если они конечны и их значения совпадают, то функция непрерывна в указанной точке, для нахождения предела надо сделать замену
,если они конечны и их значения совпадают, то функция непрерывна в указанной точке, для нахождения предела надо сделать замену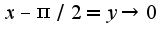 т.к. пределы равны единице(оба), то функция непрерывна в д.т.
т.к. пределы равны единице(оба), то функция непрерывна в д.т.