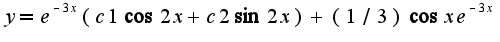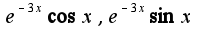| Автор | Сообщение |
|---|---|
|
Настена
#
16 июн 2008 |
|
|
Настена
#
16 июн 2008 |
|
|
Настена
#
16 июн 2008 |
|
|
Настена
#
16 июн 2008 |
|
|
О.А.
#
16 июн 2008 |
|
|
Настена
#
16 июн 2008 |
|
|
О.А.
#
16 июн 2008 |
|
|
Настена
#
16 июн 2008 |
|
|
Настена
#
16 июн 2008 |
|
|
Настена
#
16 июн 2008 |
|
|
О.А.
#
16 июн 2008 |
|
|
Настена
#
16 июн 2008 |
|
|
Настена
#
17 июн 2008 |
|
|
О.А.
#
17 июн 2008 |
|
|
Настена
#
17 июн 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
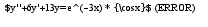
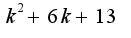
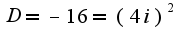 =>
=> 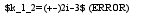 как здесь должно выглядеть однородное уравнение?
как здесь должно выглядеть однородное уравнение?
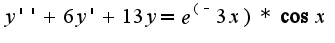

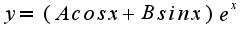
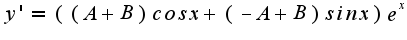
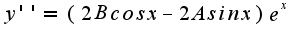 это верно?
это верно?
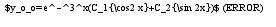 частное решение неоднородного уравнения
частное решение неоднородного уравнения
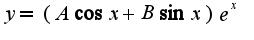
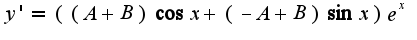
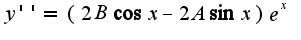 подставляем в исходное
подставляем в исходное
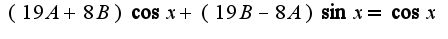 а вот подсчет A и B затруднился тем, что коэффиценты не позволяют увидеть целые числа... а при домножении вообще фигня какая-то выходит...
а вот подсчет A и B затруднился тем, что коэффиценты не позволяют увидеть целые числа... а при домножении вообще фигня какая-то выходит...
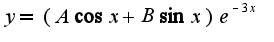 , дальнейшие действия верные, окончательный вид общего решения
, дальнейшие действия верные, окончательный вид общего решения