Поиск
| Автор | Сообщение |
|---|---|
|
маргоша
#
29 июн 2008 |
|
|
маргоша
#
29 июн 2008 |
|
|
маргоша
#
29 июн 2008 |
|
|
маргоша
#
29 июн 2008 |
|
|
О.А.
#
29 июн 2008 |
|
|
маргоша
#
29 июн 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
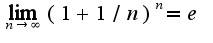 Получим, что
Получим, что 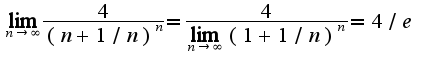 2)
2)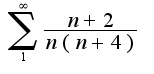 используя метод выделения главной части,пролучим
используя метод выделения главной части,пролучим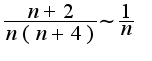 при
при 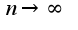 , а т.к. ряд
, а т.к. ряд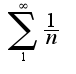 -расходится, то расходится и исходный
3)условие непонятно написано
-расходится, то расходится и исходный
3)условие непонятно написано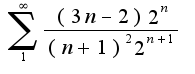 ?это выражение можно упростить, сокращая на
?это выражение можно упростить, сокращая на