Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Поиск| Автор | Сообщение |
|---|---|
|
О.А.
#
27 мар 2009 |
|
|
Аня
#
28 мар 2009 |
|
|
О.А.
#
28 мар 2009 |
|
|
Катя
#
29 мар 2009 |
|
|
О.А.
#
29 мар 2009 |
|
|
Катя
#
29 мар 2009 |
|
|
О.А.
#
29 мар 2009 |
|
|
Сергей
#
31 мар 2009 |
|
|
Сергей
#
31 мар 2009 |
|
|
О.А.
#
31 мар 2009 |
|
|
Kitsune
#
10 июн 2009 |
|
|
О.А.
#
10 июн 2009 |
|
|
Андрей
#
10 июн 2009 |
|
|
О.А.
#
10 июн 2009 |
|
|
Kitsune
#
10 июн 2009 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
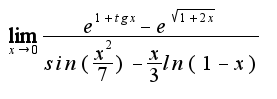 Уменя получился ответ 2,1.
Если он не верный, укажите пожалуйста правильный.. и буду искать ошибку.
Уменя получился ответ 2,1.
Если он не верный, укажите пожалуйста правильный.. и буду искать ошибку.
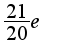
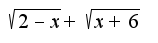 и разложить знаменатель на линейные множители, ответ 1/10
и разложить знаменатель на линейные множители, ответ 1/10
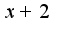 и подставьте предельную точку
и подставьте предельную точку
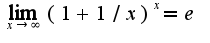 ответ
ответ 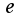
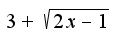
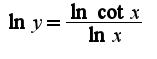 .Затем найти предел
.Затем найти предел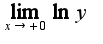 используя правило Лопиталя и потенцировать полученное выражение, ответ
используя правило Лопиталя и потенцировать полученное выражение, ответ