Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
Поиск| Автор | Сообщение |
|---|---|
|
o.a.
#
5 фев 2013 |
|
|
Pavel276
#
7 фев 2013 |
|
|
o_a
#
7 фев 2013 |
|
|
Pavel276
#
7 фев 2013 |
|
|
o_a
#
7 фев 2013 |
|
|
Pavel276
#
7 фев 2013 |
|
|
o_a
#
7 фев 2013 |
|
|
^crystal^
#
8 мар 2013 |
|
|
o_a
#
9 мар 2013 |
|
|
Viki
#
31 мар 2013 |
|
|
o_a
#
31 мар 2013 |
|
|
Viki
#
31 мар 2013 |
|
|
Маришка
#
3 июн 2013 |
|
|
o.a.
#
3 июн 2013 |
|
|
Nata
#
20 ноя 2013 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
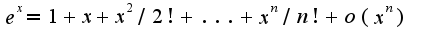
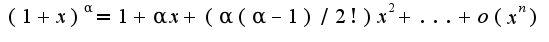
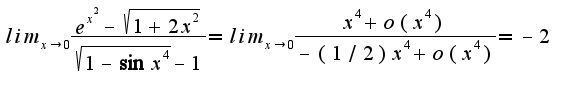 2)Во втором примере также можно использовать формулу Маклорена для функций
2)Во втором примере также можно использовать формулу Маклорена для функций 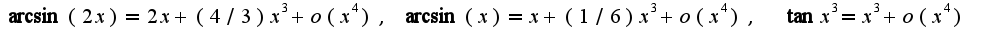
 для
для 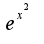 надо подставить
надо подставить 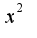 и т.д.
и т.д.
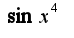 , вместо
, вместо  ---
---
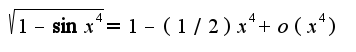 Для функции
Для функции 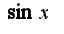 использована формула
использована формула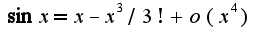
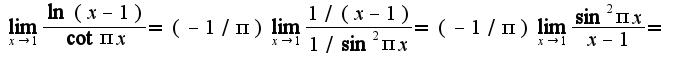
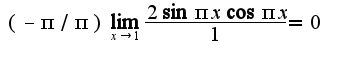 2)подобный пример решен на странице 24
2)подобный пример решен на странице 24