Поиск
| Автор | Сообщение |
|---|---|
|
Юлия
#
5 дек 2006 |
|
|
О.А.
#
5 дек 2006 |
|
|
Юлия
#
5 дек 2006 |
|
|
Popeye
#
3 янв 2010 |
|
|
О.А.
#
3 янв 2010 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
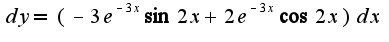
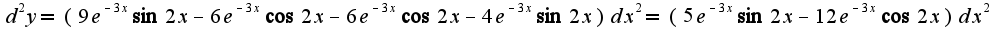
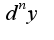 это не более чем
это не более чем 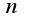 -ная производная, помноженная на
-ная производная, помноженная на 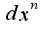 ?
И других вариантов производной быть не может? Т.е. у меня задание: найти
?
И других вариантов производной быть не может? Т.е. у меня задание: найти 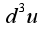 Что-то другое не может иметься в виду?
Что-то другое не может иметься в виду?
 -независимая переменная, то
-независимая переменная, то