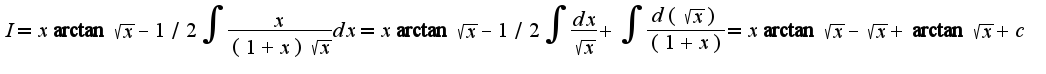| Автор | Сообщение |
|---|---|
|
Анна Каренина
#
4 ноя 2004 |
|
|
О.А.
#
4 ноя 2004 |
|
|
О.А.
#
4 ноя 2004 |
|
|
О.А.
#
4 ноя 2004 |
|
|
Станислав Матвеев
#
9 мар 2005 |
|
|
О.А.
#
10 мар 2005 |
|
|
Станислав Матвеев
#
10 мар 2005 |
|
|
О.А.
#
10 мар 2005 |
|
|
Алексей
#
11 мар 2005 |
|
|
О.А.
#
11 мар 2005 |
|
|
Станислав Матвеев
#
14 мар 2005 |
|
|
О.А.
#
14 мар 2005 |
|
|
Станислав Матвеев
#
15 мар 2005 |
|
|
О.А.
#
15 мар 2005 |
|
|
Алексей
#
20 мар 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
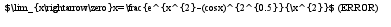
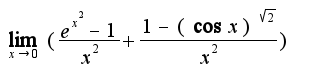 А затем используем два известных предела:
А затем используем два известных предела:
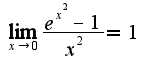 и
и 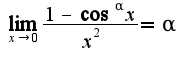 (второй предел решали на последнем занятии в понедельник). Следовательно, получим
(второй предел решали на последнем занятии в понедельник). Следовательно, получим
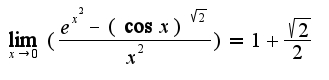 Кстати в выражении, которое Вы набрали есть синтаксические ошибки, посмотрите правильную запись
$\lim_{x\rightarrow 0}(\frac{e^{x^{2}}-(\cos x)^{\sqrt{2}}}{x^{2}})$
Кстати в выражении, которое Вы набрали есть синтаксические ошибки, посмотрите правильную запись
$\lim_{x\rightarrow 0}(\frac{e^{x^{2}}-(\cos x)^{\sqrt{2}}}{x^{2}})$
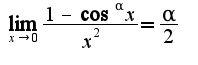
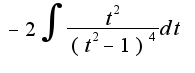 , который получается после применения подстановки
, который получается после применения подстановки 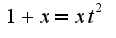 , можно использовать разложение на простейшие дроби и вычислять 8 коэффициентов, а можно использовать метод Остроградского, суть которого в следующем:
справедливо соотношение
, можно использовать разложение на простейшие дроби и вычислять 8 коэффициентов, а можно использовать метод Остроградского, суть которого в следующем:
справедливо соотношение 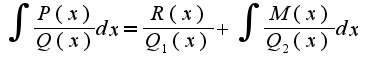 , где
, где 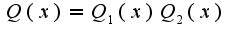 , где все корни
, где все корни 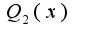 - все простые и являются корнями
- все простые и являются корнями 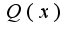 , а корни
, а корни 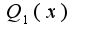 есть корни
есть корни 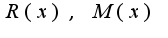 - многочлены с неопределенными коэффициентами, степени которых соответственно на единицу меньше степеней многочленов
- многочлены с неопределенными коэффициентами, степени которых соответственно на единицу меньше степеней многочленов
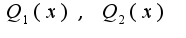 Подробное решение и нахождение неопределенных коэффициентов приведено по адресу
http://www.isu.ru/facs/math/kafedra/matan/docs/p.html
Подробное решение и нахождение неопределенных коэффициентов приведено по адресу
http://www.isu.ru/facs/math/kafedra/matan/docs/p.html
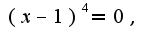 здесь кратность корня
здесь кратность корня 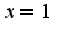 равна четырем.
равна четырем.
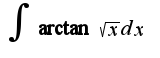 , то по частям:
, то по частям:
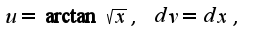 .
.