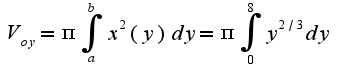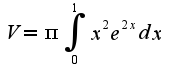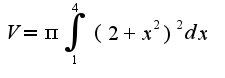Форумы > Консультация по матанализу > Вычислить объем тела, образованного вращением вокруг оси координат...

Страницы: 1 2

Поиск
Автор Сообщение
Станислав #
10 ноя 2008
Привет. Вот задали по математике типовик. НЕмогу решить 3 задания. Одно из них Вычислить объем тела, образованного вращением вокруг оси координат фигуры, ограниченной заданными линиями. y=x^3 x=0 y=8 Вокруг оси OY Заранее спасибо
О.А. #
8 июл 2008
объем вычисляется по формуле$V_{oy}=\pi\int_{a}^{b}x^2(y)dy=\pi\int_{0}^{8}y^{2/3}dy$
Станислав #
11 июн 2009
спасибо, будем решать
Dutyfree #
сегодня в 15:32
Привет ! помогите решить задание по математике :Вычислить объем тела образованного вращением фигуры ограниченной линиями y=sinx x=o y=1 вокруг оси OY
О.А. #
сегодня в 18:45
формула для вычисления объема написана выше
Dutyfree #
19 ноя 2008
Плиз нарисуй рисунок
О.А. #
2 июн 2008
http://matan.isu.ru/kons112.gif
Dutyfree #
17 ноя 2008
Большое спасибо)
Алексей #
сегодня в 02:20
Добрый вечер! Подскажите пожалуйста, как будет выглядеть формула, если вращение происходит по ОХ. Графики функций - y=x*(e в степени x), y=0, x=1
О.А. #
15 июн 2008
здравствуйте. формула для вычисления объема тела вращения вокруг оси OX имеет вид$V=\pi\int_{0}^{1}x^2e^{2x}dx$
Андрей Викторочич #
13 ноя 2008
Добрый вечер! Друзья, помогите вычислить объем тела, образованного вращением фигуры, ограниченной линиями y=2+x^2, x=4, x=1, x=корень из(y-2) вокруг оси OX.
О.А. #
28 июн 2009
$V=\pi\int_{1}^{4}(2+x^2)^2dx$
MIXer #
26 ноя 2008
Помогите плиз формулу составить. y=arcsinx, y=arccosx и y=0. С рисунком кое-как разобрался. Интеграл от 0 до п/4.
Анастасия #
сегодня в 01:07
Помогите пожалуйста.завтра экзамен.мне нужны краткие ответы на некоторые вопросы: 1) объём тела вращения. 2)площадь поверхности тела вращения 3)Теоремы Лагранжа.Геометрический смысл теоремы. заранее спасибо!
О.А. #
сегодня в 09:36
этот материал есть в любом учебнике по математическому анализу, например, Садовничий В.А. "Математический анализ"

Страницы: 1 2

Форумы > Консультация по матанализу > Вычислить объем тела, образованного вращением вокруг оси координат...
Чтобы написать сообщение, необходимо войти или зарегистрироваться

© teacode.com, 2004-2016