| Автор | Сообщение |
|---|---|
|
Dan
#
19 дек 2011 |
|
|
абвгдейка
#
14 янв 2012 |
|
|
o.a.
#
15 янв 2012 |
|
|
абвгдейка
#
15 янв 2012 абвгдейка
15 янв 2012
|
|
|
o.a.
#
16 янв 2012 |
|
|
абвгдейка
#
16 янв 2012 |
|
|
o.a.
#
17 янв 2012 |
|
|
абвгдейка
#
19 янв 2012 |
|
|
o_a
#
20 янв 2012 |
|
|
абвгдейка
#
22 янв 2012 |
|
|
o_a
#
22 янв 2012 |
|
|
абвгдейка
#
22 янв 2012 |
|
|
o_a
#
22 янв 2012 |
|
|
абвгдейка
#
23 янв 2012 |
|
|
o_a
#
23 янв 2012 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
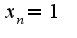
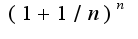 сходится на основании теоремы Вейрштрасса,т.е. является возрастающей и ограниченной
Доказательство критерия Коши дано в учебнике по математическому анализу под редакцией Зорича В.А., если у Вас есть вопросы(конкретные)
по доказательству, то я с удовольствием на них отвечу
вопроc N14 надо изучить самостоятельно, можно воспользоваться учебным пособием
http://matan.isu.ru/matan/index.html
учитывать, что пособие оптимизировано под IE
сходится на основании теоремы Вейрштрасса,т.е. является возрастающей и ограниченной
Доказательство критерия Коши дано в учебнике по математическому анализу под редакцией Зорича В.А., если у Вас есть вопросы(конкретные)
по доказательству, то я с удовольствием на них отвечу
вопроc N14 надо изучить самостоятельно, можно воспользоваться учебным пособием
http://matan.isu.ru/matan/index.html
учитывать, что пособие оптимизировано под IE
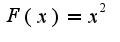 ,
, 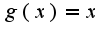
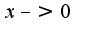
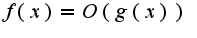 , т.к. модуль (х) <=c (к сожалению не могу написать в latex)
2.
, т.к. модуль (х) <=c (к сожалению не могу написать в latex)
2. 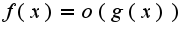 , т.к.
, т.к. 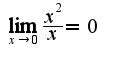
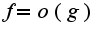 по базе
по базе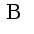 если выполнено условие:
если выполнено условие: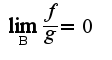
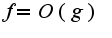 по базе
по базе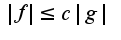 кроме того, известно свойство:Если функция бесконечно малая более высокого порядка малости, то она является и ограниченной, то есть
кроме того, известно свойство:Если функция бесконечно малая более высокого порядка малости, то она является и ограниченной, то есть 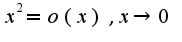 , то тем более
, то тем более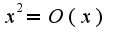 при
при 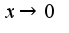
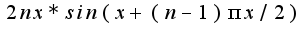 поменялось на
поменялось на 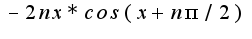 по формуле приведения ведь,но если раскрыть скобки,то у мня не получается.
2. почему
по формуле приведения ведь,но если раскрыть скобки,то у мня не получается.
2. почему 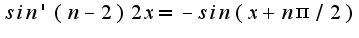 Зорич. формула Лейбница. стр 245.пример 26.Спасибо.
Зорич. формула Лейбница. стр 245.пример 26.Спасибо.
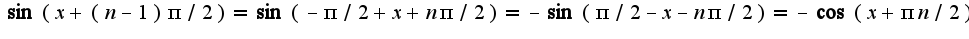 2)
2)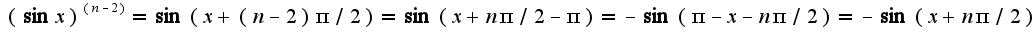
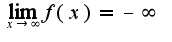 Для Любого E>0,существует б - зависящая от Е, что при любом х, х>б,выполняется условие:
Для Любого E>0,существует б - зависящая от Е, что при любом х, х>б,выполняется условие: 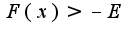 Проверьте пожалуйста верно ли последнее условие? или
Проверьте пожалуйста верно ли последнее условие? или 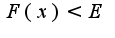 ? почему?
? почему?
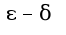 следующим образом:
следующим образом: 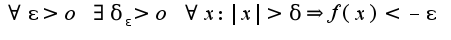 , так как модуль от функции
, так как модуль от функции 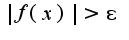 раскрывается как
раскрывается как 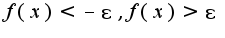 Но, поскольку предел равен минус бесконечности, то нам нужно только неравенство
Но, поскольку предел равен минус бесконечности, то нам нужно только неравенство