Поиск
| Автор | Сообщение |
|---|---|
|
Лена
#
11 ноя 2007 |
|
|
О.А.
#
11 ноя 2007 |
|
|
Лена
#
11 ноя 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
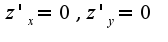 затем проводят исследование на характер экстремума(минимум, максимум)для этого составляют матрицу из вторых частных производных и если детерминант данной матрицы положительный, то экстремум существует, причем, максимум, если
затем проводят исследование на характер экстремума(минимум, максимум)для этого составляют матрицу из вторых частных производных и если детерминант данной матрицы положительный, то экстремум существует, причем, максимум, если 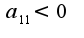 , если
, если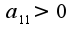 , то минимум, если детерминант отрицательный, то экстремума нет.
Для данной задачи легко установить, что точка(0,3)-максимум.
2)особой точкой данного интеграла второго рода является ноль, используем эквивалентность функций:
, то минимум, если детерминант отрицательный, то экстремума нет.
Для данной задачи легко установить, что точка(0,3)-максимум.
2)особой точкой данного интеграла второго рода является ноль, используем эквивалентность функций: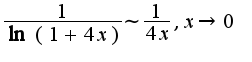 интеграл от функции
интеграл от функции 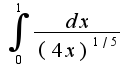 является сходящимся, потому что показатель
является сходящимся, потому что показатель 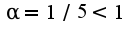 Поэтому исходный тоже сходится
Поэтому исходный тоже сходится