Поиск
люсёнок
#
1 апр 2009
|
Здравствуйте!Помогите решить пример. Дана матрица С (пишу строки)(1 2 3 -1)(-2 1 1 3)(4 3 5 -5)(3 1 2 -4)и вектор b(2 1 3 1).Используя метод элементарных преобразований Гаусса:
1) ранг матрицы С
2)общее решение однородной системы уравнения Cx=0,где x=(x1 x2 x3 x4),0=(0 0 0 0),x-вектор неизвестных,0- вектор правых частей однородной системы.Выписать решения в координатной и в векторной формах.
3)Совместна ли неоднородная система уравнений Cx=d?Если совместна найти ее общее (или единственное) решение в координатной и векторной формах.
|
люсёнок
#
1 апр 2009
|
Здравствуйте!Ольга Александровна Помогите пожалуйса решить пример. Дана матрица С (пишу строки)(1 2 3 -1)(-2 1 1 3)(4 3 5 -5)(3 1 2 -4)и вектор b(2 1 3 1).Используя метод элементарных преобразований Гаусса:
1) ранг матрицы С
2)общее решение однородной системы уравнения Cx=0,где x=(x1 x2 x3 x4),0=(0 0 0 0),x-вектор неизвестных,0- вектор правых частей однородной системы.Выписать решения в координатной и в векторной формах.
3)Совместна ли неоднородная система уравнений Cx=d?Если совместна найти ее общее (или единственное) решение в координатной и векторной формах.
Из этого всего я нашла только ранг матрицы С=2.И все.А дальше что-то затрудняюсь.Помогите!!!
|
О.А.
#
1 апр 2009
|
здравствуйте.
Ранг правильно нашли, чтобы найти решения системы однородной надо учесть, что ранг равен двум, поэтому количество произвольных констант две 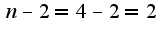 решение будет зависеть от этих произвольных констант 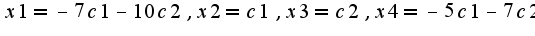 Аналогично решается и система 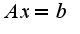 существует б.множество решений, зависящих от двух констант 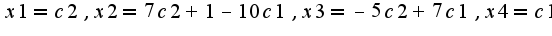 Данный материал подробно изложен в учебнике Куроша А.Г. и задачнике Проскурякова
|
люсёнок
#
1 апр 2009
|
Большое спасибо!Ну вот еще один вопрос С чего начать решения этого примера
Привести кривую второго порядка к каноническому виду ортогональным преобразованием.
XY=4
Буду очень благодарна!!!
|
О.А.
#
2 апр 2009
|
смотрите
http://www.ssga.ru/AllMetodMaterial/metod_mat_for_ioot/metodichki/iutina/2_AG.html
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
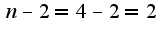 решение будет зависеть от этих произвольных констант
решение будет зависеть от этих произвольных констант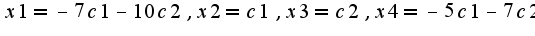 Аналогично решается и система
Аналогично решается и система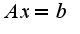 существует б.множество решений, зависящих от двух констант
существует б.множество решений, зависящих от двух констант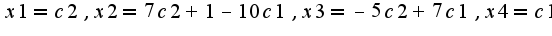 Данный материал подробно изложен в учебнике Куроша А.Г. и задачнике Проскурякова
Данный материал подробно изложен в учебнике Куроша А.Г. и задачнике Проскурякова