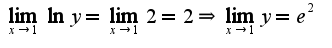| Автор | Сообщение |
|---|---|
|
Маруся
#
19 окт 2007 |
|
|
Маруся
#
19 окт 2007 |
|
|
О.А.
#
19 окт 2007 |
|
|
Лена
#
21 окт 2007 |
|
|
О.А.
#
21 окт 2007 |
|
|
Лена
#
21 окт 2007 |
|
|
Циф
#
24 окт 2007 |
|
|
О.А.
#
24 окт 2007 |
|
|
Циф
#
24 окт 2007 |
|
|
О.А.
#
25 окт 2007 |
|
|
Anatoly
#
25 окт 2007 |
|
|
О.А.
#
25 окт 2007 |
|
|
Anatoly
#
25 окт 2007 |
|
|
О.А.
#
25 окт 2007 |
|
|
Me
#
18 мар 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
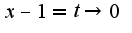 Затем использовать второй замечательный предел
Затем использовать второй замечательный предел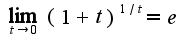 ответ
ответ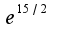
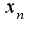 -фундаментальна, если
-фундаментальна, если 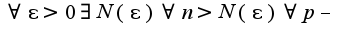 натуральном
натуральном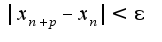 Для данной последовательности
Для данной последовательности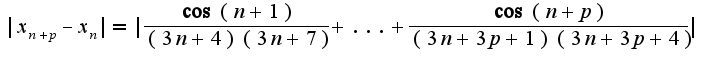 Так как модуль суммы не превосходит сумму модулей и функция косинус ограничена сверху единицей получим оценку
Так как модуль суммы не превосходит сумму модулей и функция косинус ограничена сверху единицей получим оценку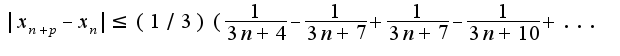
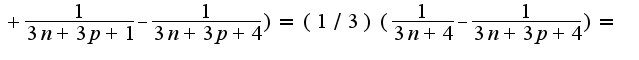
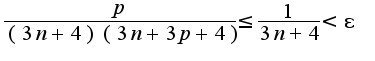 при
при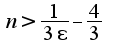 2)Чтобы записать отрицание определения, надо поменять кванторы местами и изменить знак неравенства на противоположный
2)Чтобы записать отрицание определения, надо поменять кванторы местами и изменить знак неравенства на противоположный
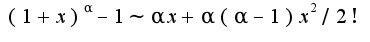 при
при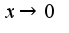 предел равен
предел равен 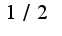 2)привести ко второму замечательному пределу(такие примеры уже разобраны в темах нашей консультации)
2)привести ко второму замечательному пределу(такие примеры уже разобраны в темах нашей консультации)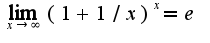 Предел равен трем.
3)Каждое слагаемое представить в виде разности
Предел равен трем.
3)Каждое слагаемое представить в виде разности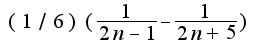
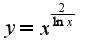 , логарифмируя, получим
, логарифмируя, получим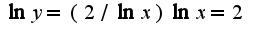 Найдем предел от данного равенства
Найдем предел от данного равенства