Поиск
| Автор | Сообщение |
|---|---|
|
Екатерина
#
26 апр 2009 |
|
|
О.А.
#
26 апр 2009 |
|
|
Екатерина
#
26 апр 2009 |
|
|
О.А.
#
26 апр 2009 |
|
|
Екатерина
#
27 апр 2009 |
|
|
О.А.
#
27 апр 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
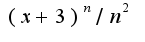 Находим радиус сходимости:
Находим радиус сходимости: 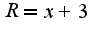 получила,что x принадлежит
получила,что x принадлежит 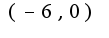 Исследуем сходимость ряда на концах: x=0
Исследуем сходимость ряда на концах: x=0 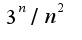 x=-6
x=-6 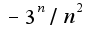 (в обоих случаях расходится??? )
Т.О. ряд сходится абсолютно при x принадлежащем (-6,0) и расходится (-беск, -6]U[0, + беск)
2) сумма по n от 1 до бесконечности
(в обоих случаях расходится??? )
Т.О. ряд сходится абсолютно при x принадлежащем (-6,0) и расходится (-беск, -6]U[0, + беск)
2) сумма по n от 1 до бесконечности 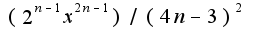
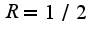 x принадлежит (-1/2,1/2).
На концах: при х=-1/2
x принадлежит (-1/2,1/2).
На концах: при х=-1/2 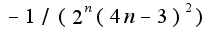 x=1/2
x=1/2 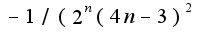 (у меня получилось что теже оба ряда расходятся)
Ряд сходится абсолютно при х (-1/2,1/2), расходится (-беск,-1/2]U[1/2, + беск)
Заранее большое спасибо!!!
(у меня получилось что теже оба ряда расходятся)
Ряд сходится абсолютно при х (-1/2,1/2), расходится (-беск,-1/2]U[1/2, + беск)
Заранее большое спасибо!!!
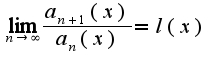 если
если 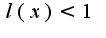 , то ряд сходится, тем самым определяется область сходимости
, то ряд сходится, тем самым определяется область сходимости
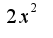 , х принадлежит (-1/корень(2), 1/корень(2)), на концах сходится, следователньо ряд сходится абсолютно на [-1/корень(2),1/корень(2)], расходится (-беск, -1/корень(2))U(1/корень(2),+беск)
, х принадлежит (-1/корень(2), 1/корень(2)), на концах сходится, следователньо ряд сходится абсолютно на [-1/корень(2),1/корень(2)], расходится (-беск, -1/корень(2))U(1/корень(2),+беск)